三角がキモなのよ・・・

今まで地球の形についてや日本の測量モデル、基準点について基本となることを説明してきたのだが、平面直角座標も比高（高さ）も測量座標を計算するのに三角関数を使うので、理解していないと座標を決定することができません。

昔みたいに関数電卓やポケットコンピューターを駆使して計算する時代ではないので、測量ソフトや土木施工管理ソフトで観測値を入力すれば計算されるし、トータルステーションならその場で座標を計算して画面に表示されるので、間違えることも少なく、現場で図面と計算機でポチポチすることがほぼ無くなった。

プログラム電卓なるものもあって、測量するうえで必要な計算式が30個くらい入っている値段の高い電卓もあった。

ポケコンにはプログラムを入力して使うのだが、プログラム言語を覚える必要があって、使いこなすまでかなりの時間を要したなぁ・・・。

スロットのプログラムを組んで授業中ずっと遊んでいたのが懐かしいです。

まぁそれはそれとして、測量座標を計算するのに三角形を理解していないと、座標も高さも計算できないことが多いのだが、数学が大の苦手だった私がどうやって計算できるようになったのか、簡単に説明したいと思います。

まず、三角形の基本を改めて理解するようにし、頭の中ですぐにイメージ出来るようにしました。

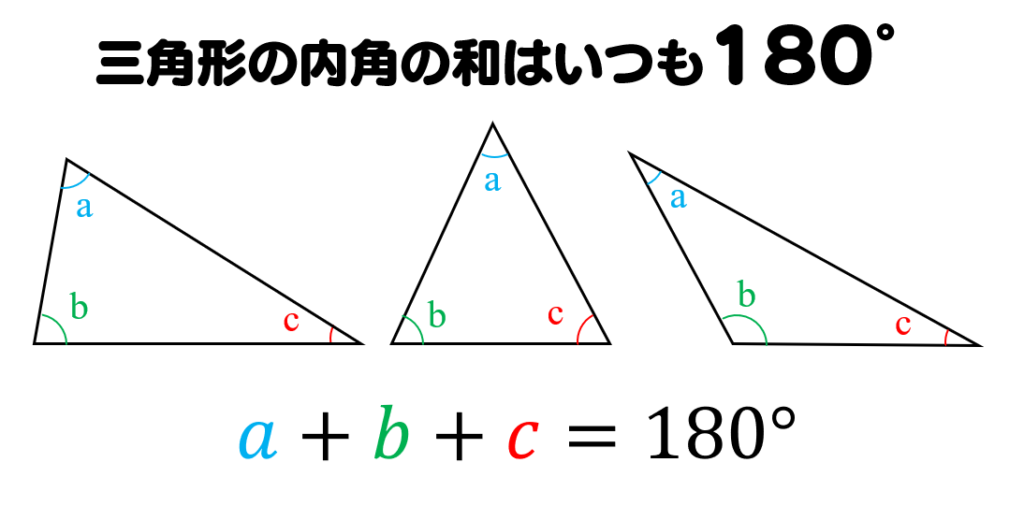
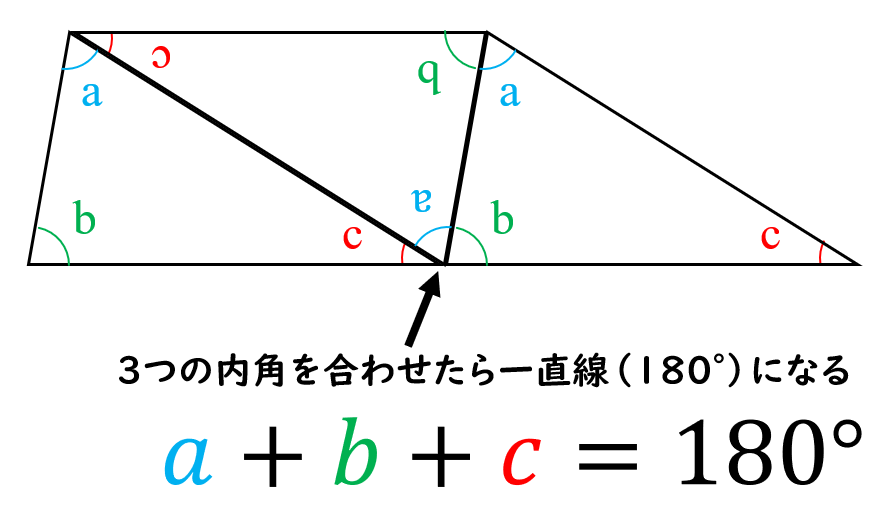
三角形の内角の和は180度。

単純に内角を足せばわかる事で小学生で習う算数なんだけど、現場と置き換えた時に三角形でイメージできないと難しい事が多いので、私はまず基本的なこの事を理解するようにしました。

次に理解しないといけないのは直角三角形での三平方の定理。

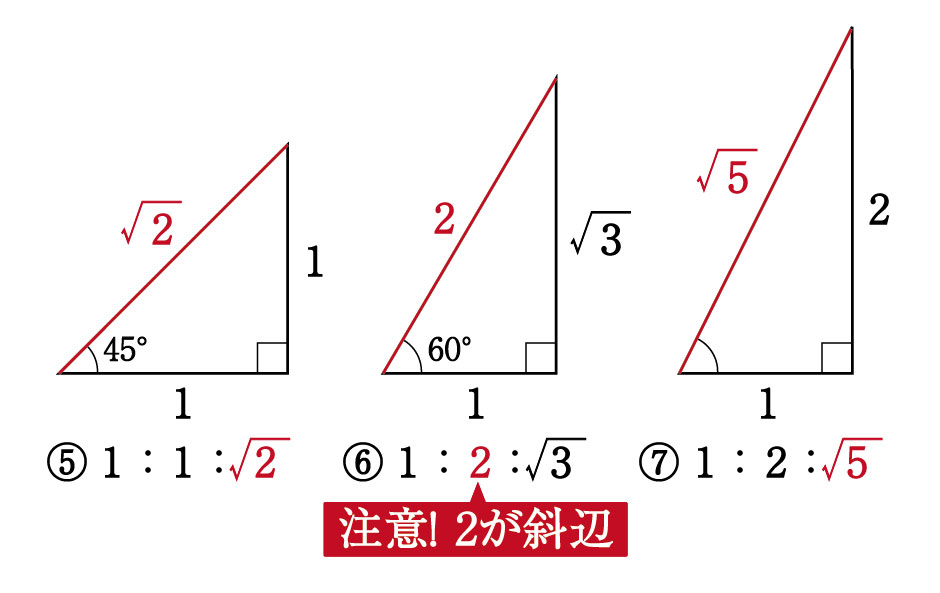
直角をはさむ2辺がわかっている時の辺（斜辺）の長さを求める公式。

直角三角形にしか当てはまらないので注意が必要なのだが、直角三角形を座標に置き換えてイメージできれば、2点間の距離を計算したい時に簡単に計算できる。

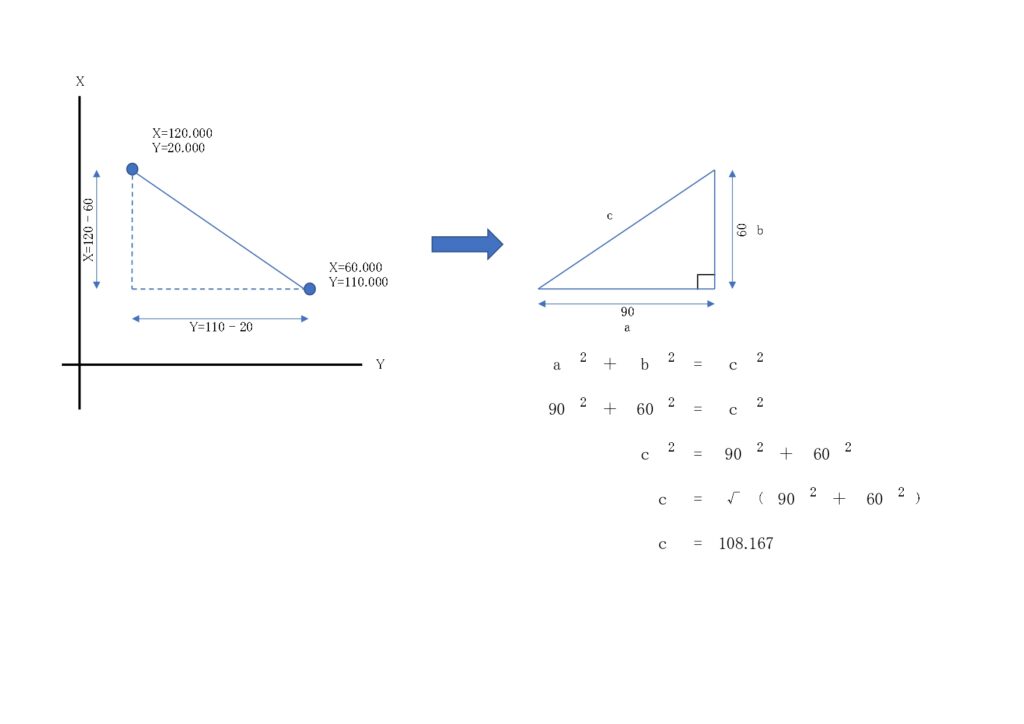
図で表すとこのようになり、XとYの座標差から直角三角形に置き換え、2点間の距離を計算することができる。

高さ（比高）に応用した場合はこちら

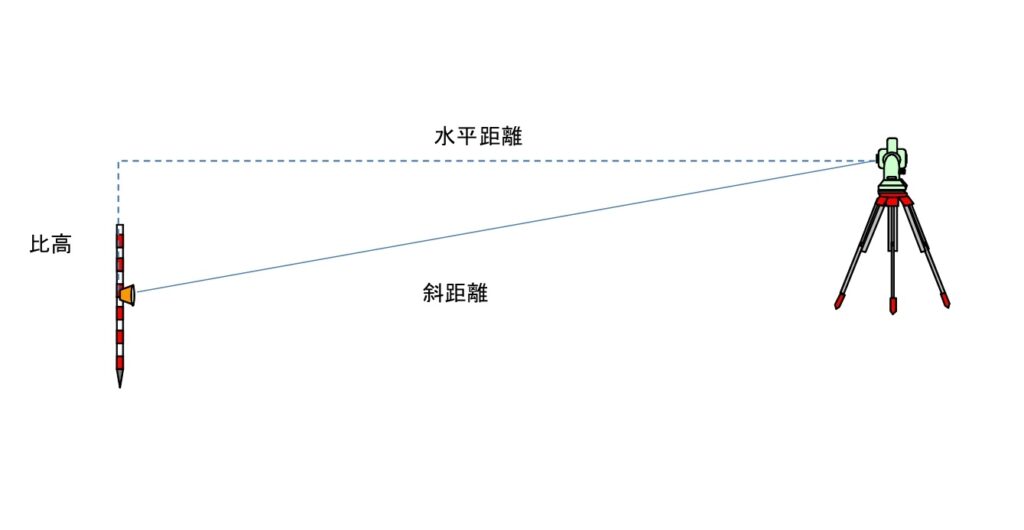
まずは基本となる三角形の性質を理解してイメージできるようになると、現場で応用が利くようになり、その場ですぐに計算でき、チェックすることも可能になる。

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

ブログランキングに参加しています。ポチっとして頂けるととても励みになります。

応援宜しくお願い致します。m(_ _"m)